N-Bulb in a Circle Puzzle

Difficulty: Medium, Asked-In: Microsoft, Bloomberg

Problem Statement

There is a circle of n lights with a switch next to each of them. Each switch can be flipped between two positions, thereby toggling the on/off states of three lights: its own and the two lights adjacent to it. Initially, all the lights are off. How can we design a strategy to turn all the lights on by flipping the minimum number of switches?

Analysis of the Problem

After reading the problem statement, the simplest thing we can do is try out some sample test cases and figure out if any pattern exists.

Trial 1: Let’s take n = 6: if we switch on the two bulbs as shown in the image below, all the bulbs will be switched on. But what sense this trial makes. Let’s see.

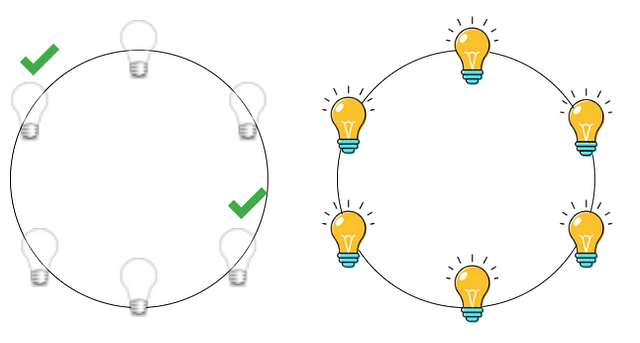
We can observe from here if for any n if we can group three such bulbs, then we can switch it on in a single go. Thus we can divide this problem into three sub-problems:

Case 1: If n%3 = 0 (n is divisible by three)

In this case, we can group three bulbs together and switch them on one by one. So for n = 6, we need two steps to switch on all the bulbs. Similarly, for any n divisible by 3 we need n/3 steps to switch on all the bulbs.

Case 2: If n%3 = 1 (Remainder 1 on dividing n by 3)

Let’s take one example to n = 7 bulbs as 7%3 = 1. Now figure out how things are working. Initially, all the bulbs are switched off. Before switching any bulb, let’s think about the strategy we must follow for switching on or off any bulb. As already we have seen in the previous case, if we have a number of bulbs which is multiple of three, we can switch it on all by grouping them in the group of 3. In this particular bulbs combination, if we group 3 bulbs together and switch them on, we will always be left with one bulb. Let’s think in a reverse way: if we could manage to switch it on that one bulb, the remaining will be switched on in one go. Try to do it yourself :) !!

So let’s discuss how we will proceed. We can follow along with the image posted below. First, we will switch on all the bulbs numbered 1 to 6, which would take 2 steps. Now our goal would be to switch on the remaining single bulb. How do we do it? Let’s think!

• If we turn off the 1st bulb, the 2nd bulbs turn off, and the 7th bulb turns on. 
• Next, if we turn off the 3rd bulb which turns on the 2nd bulb, and turns off the 4th one.
• Next, if we turn off the 6th bulb which turns off the 5th,6th, and 7th bulbs. So we reach the configuration where only one bulb is lit. 
• Now in just 2 steps, we can turn all bulbs on. Think!

So, a total of 7 steps we have required to turn all the bulbs.

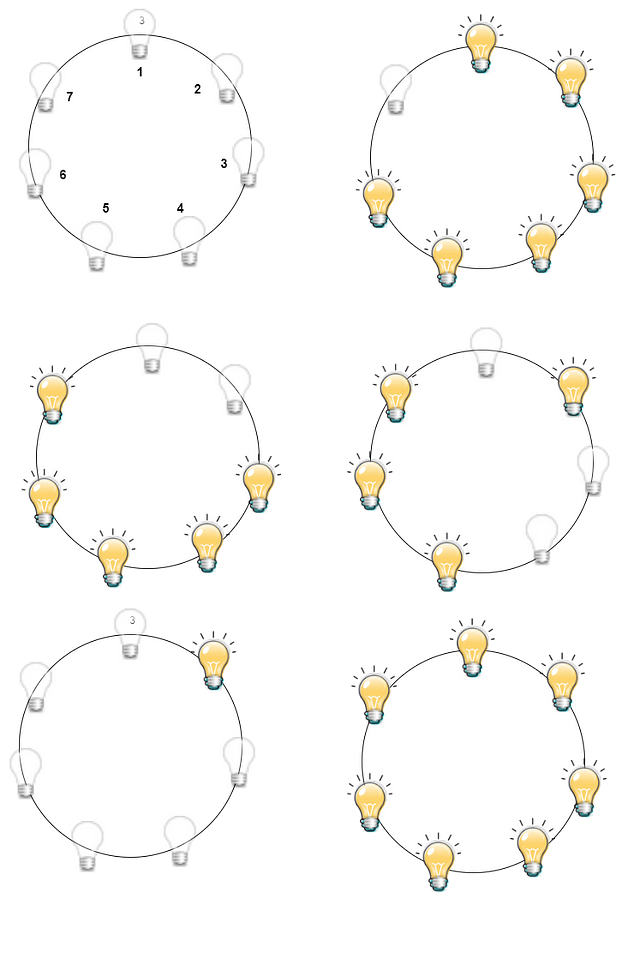
So generalizing this fact we required n steps for turning on all the bulbs such that n%3 =1. How? let’s think! Suppose n= 3k + 1.

• We need a k steps to turn on the first 3k bulbs. The last bulb will be off at this point. 
• We need k+ 1 steps to turn on the last bulb. The remaining 3k bulbs will be off at this point.
• Now finally, we again need k steps to turn on the remaining 3k bulbs. Now all the bulbs are on at this point.

So when n%3 = 1, the total number of steps to turn on all the bulbs = k+ (k + 1) + k = 3k + 1 = n

Case 3: n%3 = 2 (Remainder 2 on dividing n by 3)

For this last case, let’s take one example: n = 8 bulbs as 8%3 = 2. Let’s figure out how things will work in this case. Initially, all the bulbs are switched off as usual. Again before switching any bulb, let’s think about the strategy. In this particular bulbs combination, if we group 3 bulbs together and switch them on, we will always be left with two bulbs. What if we think in a reverse way: if we find a way to switch on those two bulbs, the remaining will be switched on in one go. Try to do it yourself :) !!

Let’s discuss how we will proceed in this case. First, we will switch on all the bulbs numbered 1 to 6, which would take 2 steps. Now our goal would be to switch on the remaining 2 bulbs. How do we do it? Let’s think!

• We switch on the 8th bulb, which will turn off the 1st bulb and turn on the 7th bulb.
• Next, we turn off the 6th and 2nd bulbs, turning off all the bulbs adjacent to them, and we will be left with only the 8th bulb turned on.
• Next switch on the 7th bulb, and yes!! We reached our goal, and we have 2 bulbs turned on.

Finally, we can switch on the remaining 6 bulbs in 2 steps.

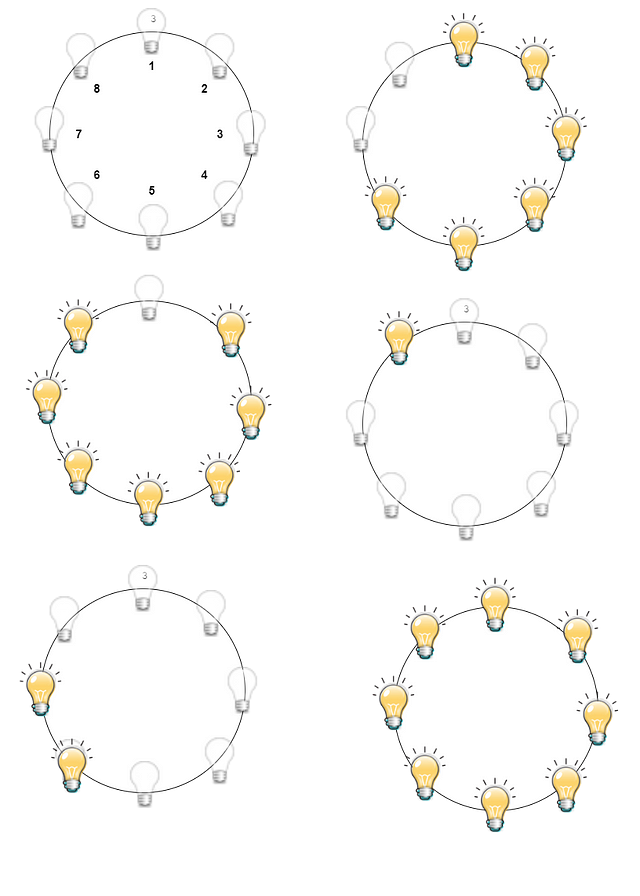
Now the interesting thing is we required only 8 steps to do so: 2 steps to turn on 6 bulbs + 1 for turning on the 8th bulb + 2 steps to turn off the 2nd and 6th bulb + 1step to turn on the 7th bulb + 2 steps to turn on the remaining bulbs. 

Again we can generalize that for n such bulbs, we require a minimum of n steps to turn all the bulbs on where n%3 = 2. let’s think! Suppose n= 3k + 2.

• We need a k steps to turn on the first 3k bulbs. The last bulb will be off at this point.
• We need k+ 2 steps to turn on the last bulb. The remaining 3k bulbs will be off at this point.
• Now finally, we again need k steps to turn on the remaining 3k bulbs. Now all the bulbs are on at this point.

So when n%3 = 2, the total number of steps to turn on all the bulbs = k+ (k + 2) + k = 3k + 2 = n

This generalization is due to the strategy we are following i.e. to lit 2 adjacent bubs and the remaining (N-2) will always be divisible by 3.

Now from all three cases, we can finally conclude that it requires N/3 steps to lit all the bulbs if N is divisible by 3 else we will require N steps always.

Try these two variations of the bulb puzzle

• Turning on a Light Bulb: A light bulb is connected to n switches so that it lights up only when all the switches are closed. A push-button controls each switch; pressing the button toggles the switch, but there is no way to know the state of the switch. Design an algorithm to turn on the light bulb with the minimum number of button pushes needed in the worst case.
• Bulb Switcher: There are n bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb. In the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the ith round, you toggle every i bulb. For the nth round, you only toggle the last bulb. Return the number of bulbs that are on after n rounds.

Enjoy learning, Enjoy Mathematics!