You’ve got someone working for you for seven days and a gold bar to pay him. The gold bar is segmented into seven connected pieces.
You must give them a piece of gold at the end of every day. What is the fewest number of cuts to the bar of gold that will allow you to pay him 1/7th each day?
We have only one gold bar and we have to pay equally for seven days. One obvious solution one can propose is 7 equal cuts in the golden bar and give 1/7 of the golden bar each day. But will that be the minimum? Think!
So let’s start from 1 Cut. It will give us 2 pieces of the gold bar. And to pay the worker on day 1, one will have to cut the first piece of size 1/7 and the rest will be 6/7. In such a case, we will not be able to pay the worker on day 2. So this doesn’t work.
Now moving forward with 2 Cuts. It will give us 3 pieces of gold bar. Let’s cut the pieces in such a manner so that one will be 1/7th of the whole gold bar, the second will be 2/7th of the whole gold bar, and the third will be 4/7th of the whole gold bar.
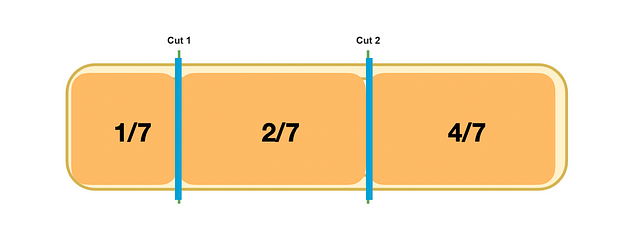
Now try to pay for 7 days with these cuts.
Day 1: We give the 1/7th gold bar to the employee. Now there are two remaining gold bars of 2/7 and 4/7 size. Total Pay = 1/7.
Day 2: We give the 2nd bar of size 2/7 on the second day and take back the 1/7 sized bar to maintain equal pay each day. Now we will have 1/7 and 4/7 sized gold bars remaining. Total Pay = 2/7.
Day 3: We give the 1/7 sized bar on the third day. Now we will have 4/7 sized gold bars remaining. Total Pay = 3/7, (2/7 + 1/7).
Day 4: We give the 3rd bar of size 4/7 and take back both 1/7 and 2/7 sized bars. Now will have 1/7 and 2/7 sized bars remaining. Total Pay = 4/7.
Day 5: We give the 1/7 sized bar. Now we will be left with a 2/7 sized gold bar. Total Pay = 5/7 (4/7 + 1/7).
Day 6: We give the 2/7 sized bar and take back the 1/7 sized bar. Now we will have a 1/7 sized bar. Total Pay = 6/7, (4/7 + 2/7).
Day 7: On the final day, we give the last piece of a bar of size 1/7. Total Pay = 7/7 (4/7 + 2/7 + 1/7).
So in only 2 cuts, we have paid the employee in gold bars giving him equal pay each day. Hence minimum cuts that will be needed to pay equally for 7 days will be 2.
Enjoy learning, Enjoy algorithmic thinking!
Just like programming, math is one of the core parts of learning data structures and algorithms. We mainly use math to analyse efficiency of various algorithms. But sometimes, the problem itself contains mathematical property or requires some mathematical insight to find a solution.
The summation formulas are used to calculate the sum of the sequence. In this blog, we have discussed the visual proofs: the sum of numbers from 1 to n (arithmetic series), the sum of infinite geometric series, the sum of squares of numbers from 1 to n, etc.
Given two non-negative integers, m and n, we have to find their greatest common divisor or HCF. It is the largest number, a divisor of both m and n. The Euclidean algorithm is one of the oldest and most widely known methods for computing the GCD of two integers.