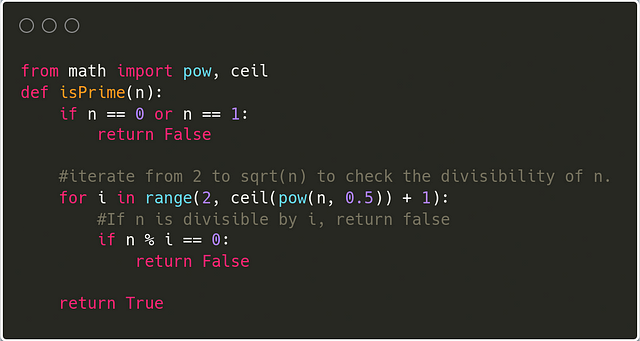
Check if a number is prime or not: Primality Test

Difficulty: Medium, Asked-in: Amazon, VMWare

Problem Description and Insights

Given a positive integer n, write a program to check if the number is prime or not.

A number x is a factor of another number y if x divides y, i.e., y % x = 0.
A number n > 1 is said to be a prime number if 1 and n are its only factors. In other words, a prime number is a number that is divisible only by two numbers itself and one.
A number n > 1 is considered composite if it has at least one more factor. In other words, A composite number is a number that can be divided by more than two numbers.
The idea of prime factorization: For every number n > 1, there exists a unique prime factorization of the number, i.e., n is expressed as the product of distinct primes that are the factors of the number, raised to some positive exponent. n = (p1^x1) * (p2^x2) …. * (pn ^ xn), where p1,p2,….,pn are distinct primes that are factors of the number with respective exponents (positive integers) x1,x2,….,xn.

In many problems, we need to check if a given number is prime or we need to find prime numbers in a range. In this blog, we will learn how to check prime numbers optimally.

A brute force approach

One basic idea would be to iterate from 2 to n - 1 and check if any n is divisible by any number. If yes, then we conclude that the given number is not prime. The time complexity of this approach is O(n), as we will iterate through n-2 numbers at max.

Check if a number is prime or not brute approach python code

An efficient approach by reducing the number of loop iterations

Now the critical question is: Can we try to optimize this approach: Is it necessary to iterate through all the n-2 numbers? For example, any integer n can be written as n = a * b, where a and b are equal if n is a perfect square and a = sqrt(n). So if we know one factor a, the other factor will be n/a.

We claim that at least one of a or b cannot be greater than sqrt(n). As if both are greater than sqrt(n), a*b > n, a contradiction. So from this argument, we conclude that it is enough for us to check the divisibility of numbers from 2 to sqrt(n), as if there is a number between 2 to n-1, which divides n, then we are sure that either it will be less than sqrt(n) or it will have another factor, n/number, which is less than or equal to sqrt(n).

The time complexity of this approach is O(sqrt(n)), as we will iterate through sqrt(n) numbers at max. Space complexity is O(1) because constant extra space is used to store variables.

Check if a number is prime or not efficient approach python code

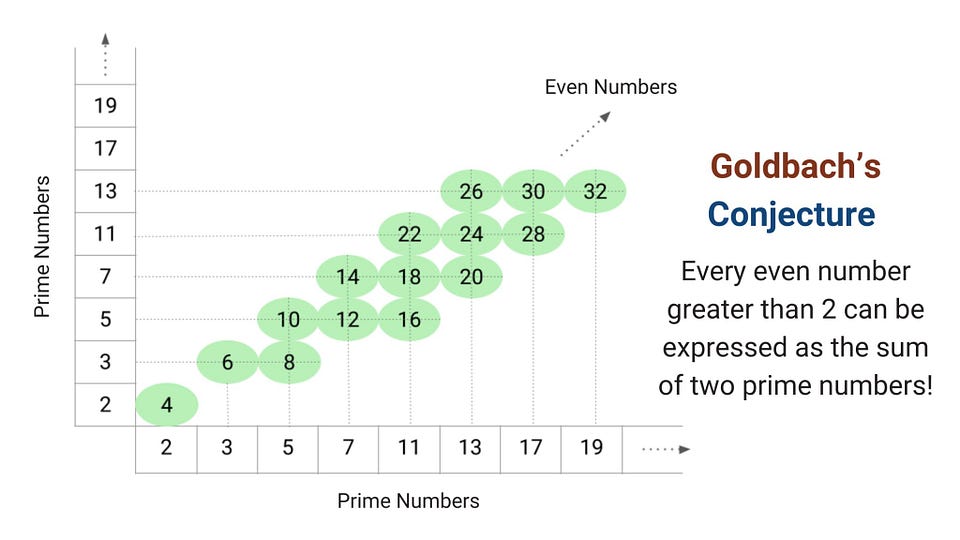
Here are two important conjectures related to prime numbers.

Goldbach Conjecture

All even natural numbers(> 2) can be represented as the sum of two prime numbers. 2 is the exceptional case here. The mathematician Christian Goldbach first proposed this conjecture in a letter to the mathematician Leonhard Euler in 1742. It is one of the best-known unsolved problems in number theory.

Goldbach Conjecture Visualization

Lemoine's conjecture

Lemoine’s conjecture is also an unsolved problem in number theory. It has puzzled mathematicians for the last 125 years. Lemoine’s conjecture is as follows: an odd integer n (where n > 5) can be represented in the form of (odd prime + even semiprime).

An odd prime is a prime number greater than 2. In other words, there is only a single even prime number which is 2.
A number is said to be a semiprime if it can be represented as a product of two prime numbers.

In mathematical terms, n = p + 2q always has a solution in primes p and q (not necessarily distinct) for n > 5. For example, we can write 47 in the form of 13 + 2 × 17 or 37 + 2 × 5 or 41 + 2 × 3 or 43 + 2 × 2.