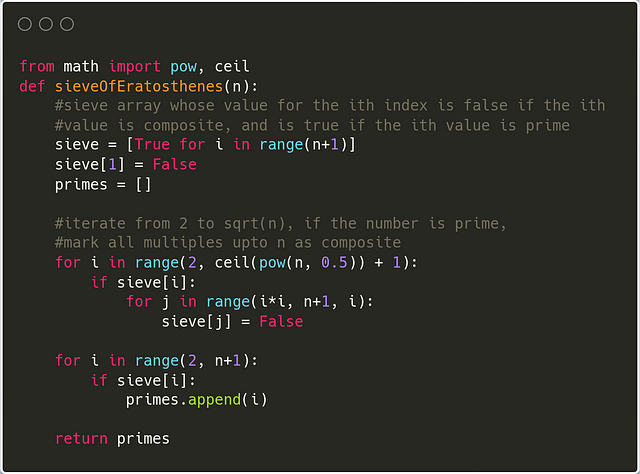
Find prime numbers in a range: Sieve of Eratosthenes

Suppose we want to find all the prime numbers between 2 and n. The brute force approach to this problem is to iterate through all the numbers in the range and check if that number is prime or not using the approach discussed in this blog. 

The time complexity of this approach is O(n*sqrt(n)). We can do better. We are not making use of the already processed numbers. For example, suppose we conclude that a number x in our range is prime by some method, then we are sure that all the multiples of x in our range are not prime numbers. Using pre-computed prime numbers to eliminate its multiples in the range is known as the Sieve of Eratosthenes.

Sieve of Eratosthenes

This algorithm finds all primes numbers from 2 to n. We assume that all the numbers in this range are prime at the start, i.e. mark them as potential candidates for prime numbers. In the following steps, we look at the first marked number, considering this to be a prime number. Then we unmark all the multiples of this number in our range, as we are sure that those numbers are not prime numbers. As the prime factors of a number are bounded by sqrt(n), we can limit our iterations to sqrt(n) starting from 2.

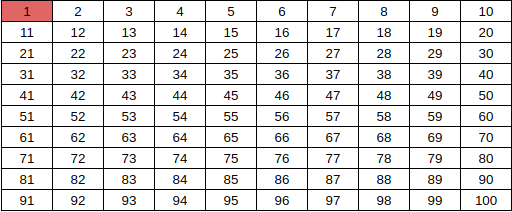
We will start from 2 [first marked number] and unmark all the multiples of the 2 till 100.

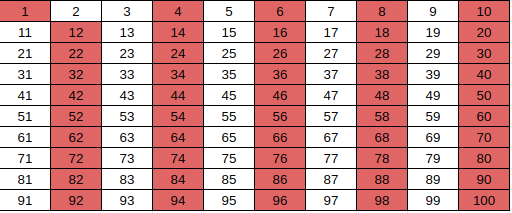
Then we start with 3 (the next marked number) and unmark all multiples of 3 till 100.

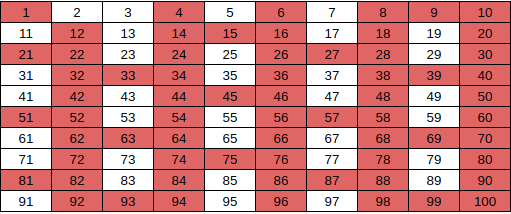
Similarly, do this for 5 and 7 as they are marked numbers less than sqrt(100). After this, the marked numbers are the prime numbers from 1 to 100.

The time complexity of the Sieve of Eratosthenes

To remove the composite numbers, we unmark the multiples of the current prime number. Now let us assume our current prime number is 2. In the first iteration, we will unmark n/2 elements. When our current prime number is 3, we unmark n/3 numbers. The total number of times we run the loop would be equal to:

n/2 + n/3 + n/5 + n/7 + n/11 + ……
= n*( 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + ……)

Using Harmonic Progression of the sum of primes, it can be proved that:

( 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + ……) = log(log(n))

Therefore, the total time complexity of the Sieve of Eratosthenes algorithm is O(nlog(log(n))).

Segmented Sieve

The segmented sieve algorithm is also used to find all prime numbers from 1 to n or all the primes in a given range. A segmented sieve is an optimization in memory usage over a simple sieve, which makes it helpful in finding primes from 1 to n efficiently compared to a simple sieve. We divide the range from 1 to n into smaller segments, and we find the prime numbers for those segments separately. The division of the whole range into segments allows us to keep one segment in memory at a time instead of loading the entire range into memory.

Algorithm Idea

1. Find all prime numbers from 1 to sqrt(n) using a simple sieve.
2. We divide the whole range(1, n) into ceil(n/sqrt(n)) number of segments, each of size sqrt(n).
3. For every segment, we perform a sieve.
4. Start and end are the first and last elements of the current segment.
5. We create an array of size end-start+1 and initially mark all the values in the array. Then similar to the previous algorithm, we iterate through all the primes found through the simple sieve, and for each marked number, unmark all its multiples within the range of the current segment.

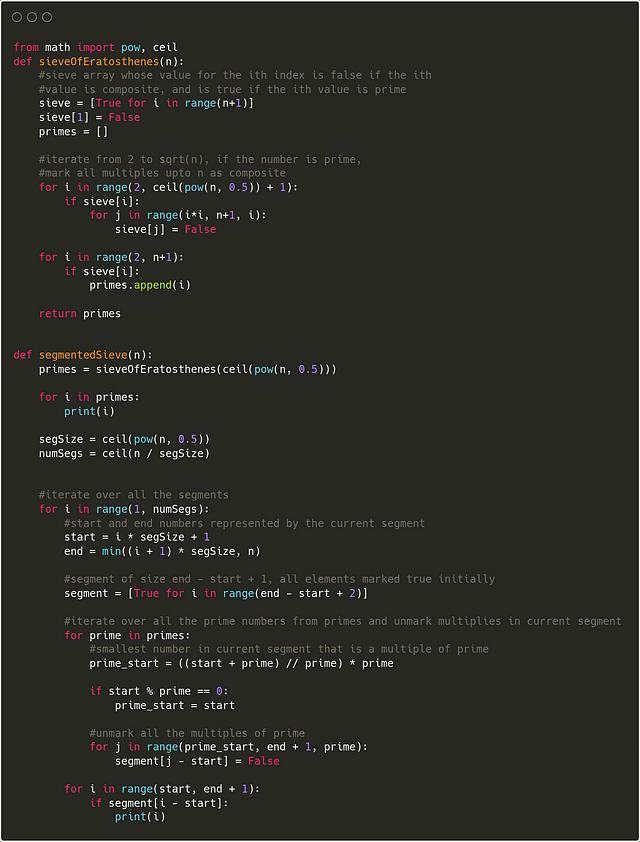
The time and space complexity for the segmented sieve is the same as that of the simple sieve.

Finding primes in a range: Sometimes we need to find all prime numbers in a range [l, r] of small size (r -l + 1 <= 10⁵), but l and r can be very large(10¹²). To solve such problems, we use the idea of the Segmented sieve. We generate all prime numbers up to sqrt(r) and use those primes to mark all composite numbers in the segment [l, r]. Explore and think!

Enjoy learning, enjoy mathematics, enjoy algorithms!