For i = 1 to n, Sum of Cubes is Equal to Square of the Sum

Problem Statement

Prove that the sum of the cubes of the first n positive integers is equal to the square of the sum of the first n positive integers. How can we do this? Let's think!

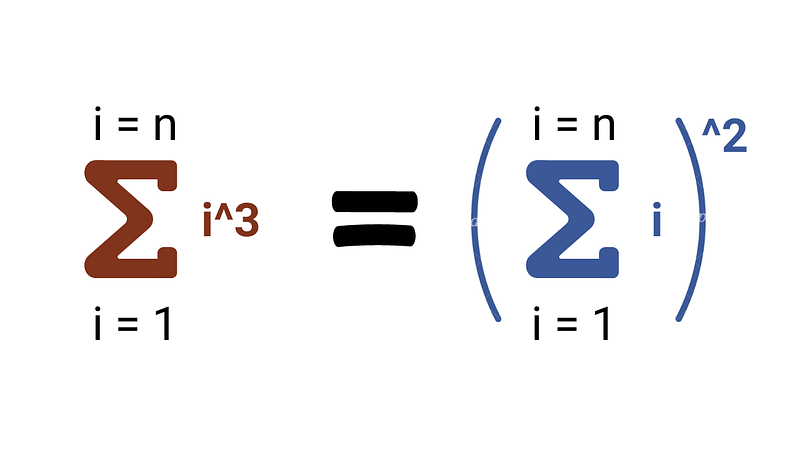Proof using Induction

If there is such types of complex relation in terms of n, we can think to apply the powerful idea of mathematical induction. To proceed with the inductive proof, we need to first set the inductive hypothesis: Suppose the above equation holds true for n i.e. 1³ + 2³ + 3³ + … + n³ = (1 + 2 + 3 + … + n )². Now we need to prove that if the equation holds for n, it also holds true for n + 1 =>

1³ + 2³ + 3³ + … + n³ + (n + 1)³ = (1 + 2 + 3 + … + n + (n + 1))²

Now our goal is to prove that left-hand side (LHS) and right-hand side (RHS) are equal. For this, we can simplify the RHS of the equation. Here LHS = 1³ + 2³ + 3³ + … + n³ + (n + 1)³, and RHS = (1 + 2 + 3 + … + n + (n + 1))².

Suppose, A = 1 + 2 + 3 + … + n, and B = n + 1.

Now RHS = (A + B)² = A² + B² + 2AB = (1 + 2 + 3 + … + n)² + (n + 1)² + 2(n + 1)(1 + 2 + 3 + … + n) 

As we know from inductive hypothesis (1 + 2 + 3 + … + n)² = 1³ + 2³ + 3³ + … + n³.

Now RHS = 1³ + 2³ + 3³ + … + n³ + (n + 1)² + 2(n + 1)((1 + 2 + 3 + … + n).

As we know, 1 + 2 + 3 + … + n = n(n + 1)/2

Now RHS = 1³ + 2³ + 3³ + … + n³ + (n + 1)² + 2(n + 1)n(n + 1)/2 = 1³ + 2³ + 3³ + … + n³ + (n + 1)² *(1 + n) = 1³ + 2³ + 3³ + … + n³ + (n + 1)³ = LHS

Both LHS and RHS hold true for n + 1. So above equation will hold true for all positive integers n by induction. The best thing is: One can apply the idea of mathematical induction to prove several complex theorems in computer science and math. Enjoy and explore!

Similar question to practice using induction

• Prove that, (for i = 1 to n) sum of i*(i + 1) = n(n + 1)(n + 2)/3.
• Prove that, (for i = 1 to n) sum of (1/2)^i = 1 — (1/2)^n.
• Prove that, (for i = 1 to n) sum of i *2^i = (n — 1)*2^(n + 1) + 2.