According to the formula we all know, the sum of first n numbers is n(n+1)/2. In mathematical terms: 1 + 2 + …. + n = n(n+1)/2. But how do we get this value? Let’s understand this visually via the following image.
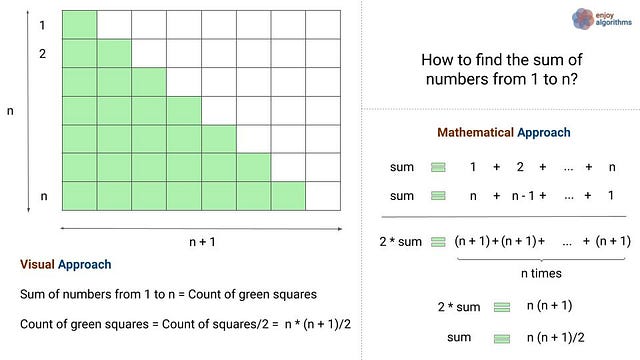
There is a popular story associated with the famous mathematician Gauss. In elementary school in the late 1700s, Gauss was asked to find the sum of the numbers from 1 to 100. The teacher assigned the question as basic project work, but Gauss found the answer quickly by discovering a pattern.
He noticed that if he split the numbers into two groups (1 to 50 and 51 to 100), he could add them together vertically to get a sum of 101.
Gauss realized then that his final total would be 50* 101 = 5050.
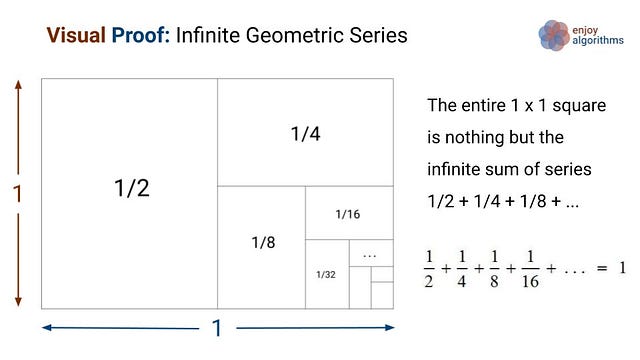
In a 1x1 square, we first cut the square in half, then cut one half in half (a quarter). Now we cut one of the quarters in half (an eighth), and so on. In such a way, we continue this process infinite times and fill up the whole square! There are two critical questions:
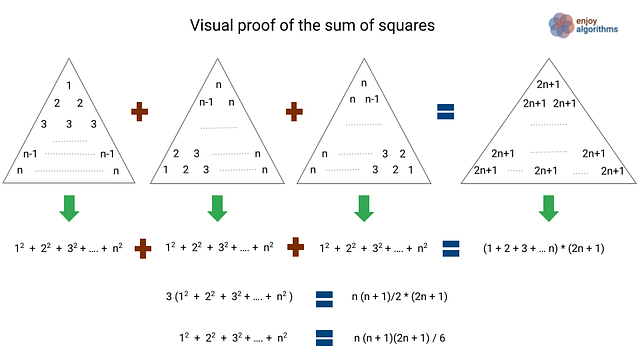
The first row of the first triangle is 1^2, the second-row sums to 2 + 2 = 2^2, the third-row sums to 3 + 3 + 3 = 3^2, and so on. That means that the sum of the numbers in the first triangle is 1^2 + 2^2 + 3^2 + ... + n^2.
The second triangle is just a 120-degree counterclockwise rotation of the first triangle. Similarly, the third triangle is a 120-degree clockwise rotation of the first triangle. In other words, the second and third triangles are the same as the first triangle. So, the sum of the numbers in the second and third triangle is also 1^2 + 2^2 + 3^2 + ... + n^2.
The sum of the three triangles in left-hand side = 3 (1^2 + 2^2 + 3^2 + ... + n^2). On the right-hand side triangle, each number in the rows is the sum of each number in corresponding rows in all three triangles, which is equal to (2n+1). So the count of (2n + 1) in the right side triangle is 1 + 2 + 3 + .... + n, which is n(n + 1)2.
Both left, and right-hand sides are equal.
=> 3 (1^2 + 2^2 + 3^2 + ... + n^2) = (2n + 1)n(n + 1)
=> 1^2 + 2^2 + 3^2 + ... + n^2 = n(n + 1) (2n + 1)/6
In case of any doubt or query, let us know your thoughts in the comment. Enjoy Mathematics.
Given two non-negative integers, m and n, we have to find their greatest common divisor or HCF. It is the largest number, a divisor of both m and n. The Euclidean algorithm is one of the oldest and most widely known methods for computing the GCD of two integers.
There are 3 doors behind which are two goats and a car. You pick door 1 hoping for the car but don’t open it right away. Monty Hall, the game show host who knows what's behind the doors, opens door 3, which has a goat. Here's the game: do you want to pick door No. 2? Is it to your advantage to switch your choice?